PERIODO DE VIGENCIA DEL PROYECTO 2023-2026

Siguiendo el artículo fundacional de Gentzen en 1935, una lógica se puede caracterizar como un cálculo de secuentes, esto es, un conjunto de reglas que conectan afirmaciones de consecuencia  (secuentes) con afirmaciones de consecuencia. Por ejemplo, a partir de la afirmación de que "A implica B" podemos derivar la afirmación de que "A y C implican B", en términos de secuentes:

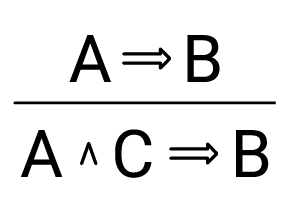
La regla nos permite movernos de un secuente a otro secuente que involucra vocabulario nuevo (en este caso, una conjunción). Otras reglas permiten introducir otras expresiones lógicas como disyunciones, condicionales o negaciones. Ahora bien, además de reglas operacionales, los cálculos de secuentes contemplan reglas que no introducen ningún vocabulario lógico. Tal es el caso, por ejemplo, de las reglas de contracción y debilitación:

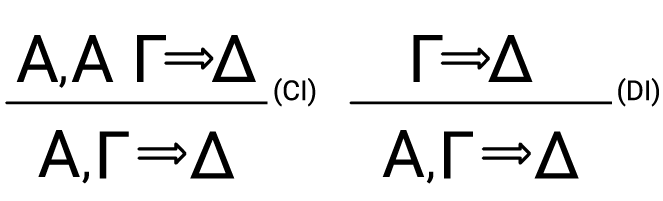
El proyecto PLEXUS, financiado por la UE, busca profundizar en nuestra comprensión del fenómeno de la subestructuralidad con particular atención a lógicas subestructurales radicales – i. e. no-reflexivas y no-transitivas.

La primera regla captura la idea de que el número de veces que afirmemos una proposición como premisa, no es relevante para la validez de un argumento. La segunda regla captura la idea de que añadir premisas a un argumento válido, da lugar a un argumento válido. Las reglas operacionales pueden verse como reglas que codifican el significado de las expresiones lógicas que introducen. Las reglas estructurales pueden entenderse como reglas que codifican una propiedad general de la propia relación de consecuencia lógica.

En el mítico artículo de Gentzen, la Lógica Clásica se caracteriza con el cálculo de secuentes conocido como LK, que involucra cierto número de reglas estructurales más cierto número de reglas operacionales. LK es el paradigma de lógica estructural: una lógica es subestructural cuando alguna regla estructural de LK falla o no válida de manera general.

En el campo de la Lógica Filosófica existen muchos argumentos en contra de la Lógica Clásica: hay muchos contextos – como la vaguedad del lenguaje natural o la existencia de paradojas – en los que la Lógica Clásica parece inadecuada para describir nuestro razonamiento. Las lógicas subestructurales proporcionan un contexto fructífero para el estudio de alternativas a la Lógica Clásica a este respecto. Además, la propia existencia de las lógicas subestructurales da lugar a preguntas filosóficas de calado acerca de la naturaleza de nuestro razonamiento, del lenguaje y del significado.

Metodología general

La metodología científica general de este proyecto es pluralista, como exige el carácter inherentemente multidisciplinar del estudio de la lógica, que requiere el uso de recursos de la filosofía (análisis e ingeniería conceptual, explicación constructiva, etc.), de la propia lógica (diseñar y aplicar diferentes sistemas de prueba, técnicas de teoría de modelos para la construcción de contraejemplos, etc.) y de varias ramas de las matemáticas (por ejemplo, álgebra y teoría de conjuntos). Además, a través del objetivo 3, el proyecto tiene un componente experimental significativo y, por lo tanto, empírico, que requiere métodos y técnicas específicos de recopilación de datos, de análisis cuantitativo y cualitativo, modelización, etc. Estos diferentes enfoques metodológicos se equilibran e integran a través de la construcción de los Work Package (WP) y la distribución de los intercambios (secondments) [28,6% en el WP1 (Fundamentos filosóficos), 47,7% en el WP2 (Lógica) y 23,5% en el WP3 (inventario y demostrador de metainferencias)].

Como se ha mencionado más arriba, los conceptos que guían la red PLEXUS son la integración (integration), la trans-fertilización (cross-fertilisation) y la transmisión del conocimiento (knowledge-sharing). Específicamente buscamos conseguir un sistema de controles y equilibrios epistémicos, apto para mitigar el riesgo de fragmentación del proyecto por sesgo y parcialidad. Por esta razón, si bien cada WP tiene una determinada característica metodológicamente dominante, esta se equilibra mediante enfoques y técnicas específicas para familias metodológicas subsidiarias y coincidentes:

W1, correspondiente al objetivo 1, tiene como finalidad sentar las bases para un análisis filosófico de la subestructuralidad, en consonancia con los desarrollos formales recientes. Su principal metodología será, por lo tanto, de naturaleza filosófica y se basará en recursos de las disciplinas filosóficas como la metafísica (análisis conceptual), filosofía del lenguaje (formalización), filosofía de las matemáticas (modelos). Se usarán métodos lógico-matemáticos (largo sensu, es decir, sistemas de prueba, teorías de equivalencia de teorías lógicas, marcos semánticos) para (i) informar y dirigir el análisis filosófico; (ii) explicitar, enriquecer y, en última instancia, verificar sus hipótesis y resultados.

WP2, correspondiente al objetivo 2, tiene un componente predominantemente formal, y se orienta hacia la producción de resultados lógico-matemáticos tales como una generalización de la semántica de la teoría de modelos y sistemas de prueba (deducción natural, cálculos secuenciales, entre otros) para lógicas radicalmente subestructurales, así como hacia el desarrollo y estudio de las teorías subestructurales de verdad, validez, fundamentación, condicionales y demás nociones relacionadas. Metodológicamente, estas tareas conducen al desarrollo de herramientas lógicas para ampliar el análisis de la subestructuralidad. De forma complementaria, el desarrollo de estas herramientas requerirá de métodos filosóficos (explicación, análisis, etc.) para (i) guiar la producción de esas herramientas y (ii) asegurar que poseen rasgos filosóficos convenientes (y exponer las deficiencias a este respecto).

WP3, correspondiente al objetivo 3, implica dificultades particulares. Este objetivo requiere adaptar las metodologías existentes en psicología cuantitativa y en ciencias de la computación a las lógicas subestructurales. La psicología cuantitativa será necesaria para construir y validar el inventario de metainferencias. El objetivo de esta herramienta psicométrica será evaluar las preferencias, sobre lógicas subestructurales en la población general. Nuestro modelo inicial es el “Free Will Inventory”, una herramienta psicométrica de 29 ítems diseñada para medir las creencias sobre el libre albedrío (determinismo, dualismo y constructos relacionados) con una buena consistencia interna y evidencias de validez del constructo. Con el fin de encontrar una formulación apropiada del inventario que proporcione información sensible sobre las inferencias de los hablantes naïve, desarrollaremos un proceso iterativo de conceptualización, diseño, pretest y seguimiento. Este proceso implica un uso esencial de ciudadanos en el diseño de la herramienta. El WP3 requiere, además, colaboración desde la informática teórica, pues busca desarrollar un demostrador automático de teoremas capaz de recoger las peculiaridades de las lógicas en estudio dentro del proyecto.

MAPA INTERACTIVO LOCALIZACIÓN DE LAS INSTITUCIONES

Pase el cursor por encima de los iconos de ubicación para ver los investigadores que pertenecen a esa institución.

UNIVERSIDAD DE NAVARRA

UNIVERSIDADE DE LISBOA, FACULDADE DE LETRAS

UNIVERSITA DEGLI STUDI DI TORINO

Ecole Normale Superieure de parís

UNIVERSITEIT VAN AMSTERDAM

THE CITY UNIVERSITY OF NEW YORK GRADUATE CENTER CUNY

UNIVERSITA DEGLI STUDI DI CAGLIARI

KING'S COLLEGE LONDON

MONASH UNIVERSITY

CONSEJO NACIONAL DE INVESTIGACIONES CIENTIFICAS Y TECNICAS (CONICET)